・tesseractとは、24個の面、32個の線分、そして16個の頂点を持つ超立方体
・4次元における立方体の拡張により生成
・物理的にtesseractを構成することは不可能であるが、3Dで視覚化することは可能
4次元空間の概念は、これまで多くの人々を魅了してきました。物理的に考えると、3次元ではxyzによって空間が認識されますが、4次元ではそこにt(時間)の概念が追加されます。しかし、抽象的な数学的観念からいえば、そこには無数の空間次元が広がっています。
そこで、4次元について考えてみましょう。幾何学の世界において、4次元のアナログ立方体はtesseractと呼ばれます。まずは、低い次元から順に確認していきましょう。
・0次元立方体:点、すなわち頂点
・1次元立方体:2つの頂点を持つ線分(各端に1点ずつ)で、頂点の拡張により生成
・2次元立方体:4つの頂点を持つ正方形で、線分の拡張により生成
・3次元立方体:8つの頂点を持つ立方体で、正方形の拡張により生成
同様に、4次元立方体(超立方体またはtesseractとも呼ばれる)は16個の頂点を持ち、立方体の拡張により生成されます。ですが、3Dの世界で生きている我々には4Dの物体を具現化することは不可能です。
つまり、立方体が正方形から成り立っているように、tesseractは立方体から成り立っているということです。24個の面、32個の線分、16個の頂点を持った物体なのです。

頂点からTesseractになるまでの物体の動き/出典:Wikipedia Commons
現実世界からかけ離れたTesseractや四次元の超立方体は視覚化が困難
不可能では無いにせよ、tesseractやその他4次元の物体を視覚化することは極めて困難です。その理由としてあげられるのは、我々は現実世界と大きくかけ離れた人工世界に耐えうるだけの想像力を持ち合わせていないからです。
また我々の脳は、2次元を3次元に置き換えられるように出来ています。すなわち、目から2次元の画像に脳は奥行きの概念を加え、視覚モデルを構築しているということです。
この機能がある故に、我々の脳は考えることに適しています。3次元の空間は、普段目にしているので視覚化しやすいのです。しかし、さらに高い次元の認識をするとなると、そのような機会がないために明確なプロトタイプが描きづらく、視覚化するとっかかりを掴めずにいるのが現状です。
物理学者と数学者は日頃から高次元で空間を認識をする訓練をしているため、他の人より脳内でそれを視覚化することに長けています。
Tesseractを視覚化してみましょう
立方体を2次元で表現出来るのであれば、tesseractを3次元で表現することも可能なはずです。
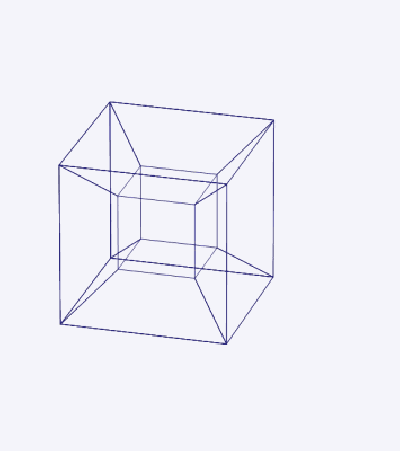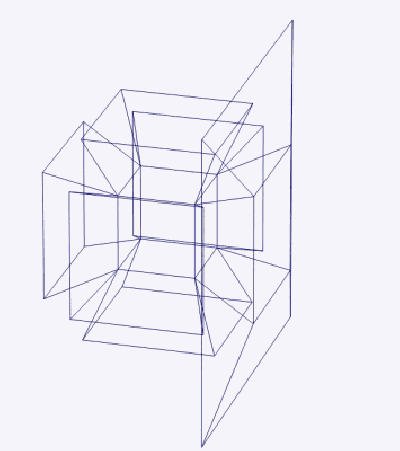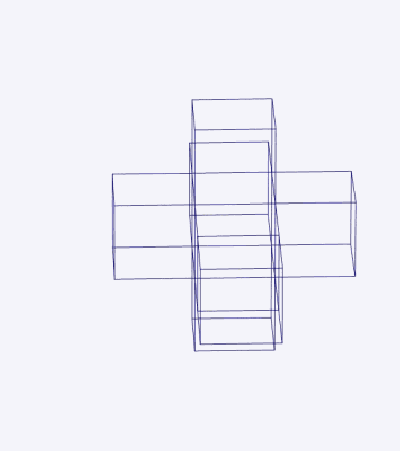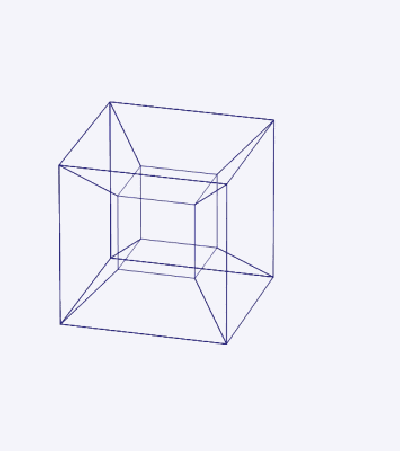
図2/画像出典:Wikipedia Commons
3Dの立方体は6個の面から出来ているように、tesseractの超立方体も8個の立方体のセルから成り立っています。
Tesseractは、3次元の空間において8個の立方体に展開可能です(図2参照)。立方体が、2次元で6個の正方形に展開されるのと同じ仕組みです。展開された幾何学物体(平らな側面)はネットと呼ばれ、Tesseractには261のネットがあると言われています。
また、4次元のローテーションには2つのタイプがあります。
1) シンプルローテーション:Tesseractの3次元プロジェクション(図3)では、平面を2等分しながら上から下、また左手前から右奥へと回転しています。

図3/tesseractの代替プロジェクション:Wikipedia Commons
2)ダブルローテーション:2つの平面が直角に交わりながら、Tesseractの3次元プロジェクション(図4)が回転しています。

図4/ tesseractの代替プロジェクション:Wikipedia Commons
さらに、隠れて見えない視点からのtesseractを描くことも可能です。例えば図5では、赤い面が4次元に一番近く、その周りは4つの立方体のセルによって囲まれているのが分かります。
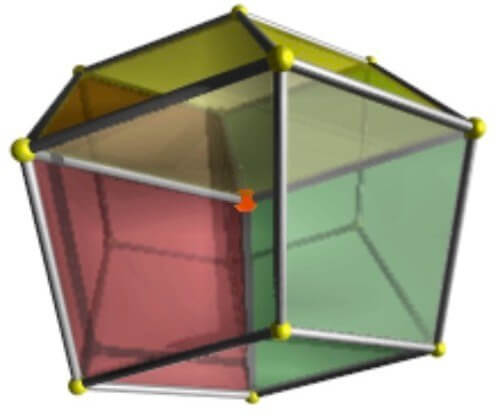
図5/隠れた視点から見るtesseract
Tesseractは1888年の著書で初めて書かれた
“tesseract”という言葉はもともと、イギリスの数学者とSF作家であるCharles Howard Hintonによって生まれました。1888年、彼は自身の著書である”A New Era of Thought”の中で初めてそれを使用しました。また、4次元に関連した新たな用語も彼が生み出しました。
それ以来、”tesseract”という言葉は芸術、建築、サイエンスフィクションの世界(AvengersやAgents of S.H.I.E.L.D)など、4次元の超立方体とは無関係な場面でも使われるようになりました。


























