6,500万光年の彼方にいるかもしれない宇宙人は、恐竜を見ているか？

6,500万光年の彼方にいる宇宙人が、地球上の恐竜を見ている可能性はあるでしょうか？ 理論的には可能です。恐竜の最後の種は、約6,500万年前に絶滅しました。そして、地球が発した当時の光は、今6,500万光年の彼方にあるのです。

 

巨大な望遠鏡を正しい方向（地球方向）に向ければ、宇宙人は恐竜を目撃することができるかもしれません。しかし、その距離から何かを捉えるには、どの程度の大きさの望遠鏡が必要なのでしょうか？ 順を追って考えてみましょう。

 

光の速度

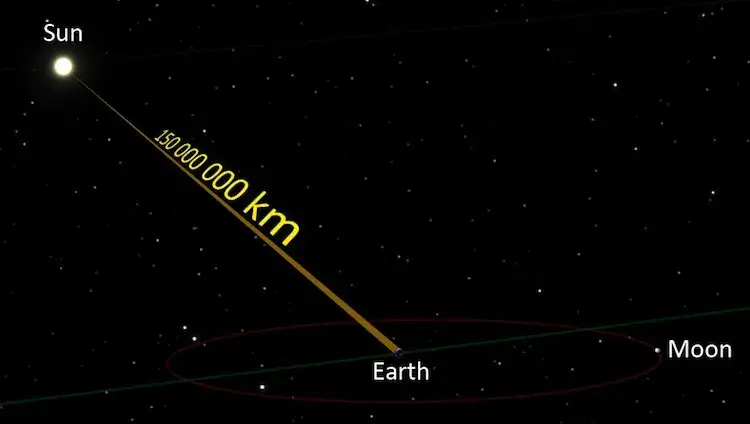
光の速度は299,792,458m/s、あるいは約300,000km/sと言われています。私たちの身の回りにあるものはすべて、光を反射しているからこそ見えており、これが一般的な光学の考え方です。今、この記事をタブレットやコンピュータで読んでいるのが、2フィート（約61㎝）の距離だとすると、実際に目にしているのはこの言葉の2ナノ秒（1ナノ秒は10億分の1秒）前の状態なのです。

 

月の場合は、その光が届くまでに1秒かかるため、私たちが見ている月は1秒前の月ということになります。しかし、太陽の場合、その差は歴然としています。地球から1億4960万kmの距離にある太陽からの光は、届くまでに8分近くかかるのです。

 

話はそれますが、もし太陽が何らかの理由で消えてしまったら、ここ地球では、次の8分間、太陽を感知することができなくなるでしょう。

 

ここで言いたいのは、何かを見るということは、技術的にはその対象が過去にどうであったかを見ることであり、それは時間に正比例する、つまり、遠ければ遠いほど、時間を遡って見ることになる、ということです。それと同じように、数百万年前に地球から出た光は、現在数百万光年先にあり、その光の中に恐竜の情報が入っているのです。

 

では、実用的なのか？

ここまでは、このテーマの理論的な可能性を論じてきました。しかし、本当に実用的なのでしょうか？ 答えは「ノー」です。宇宙は広大です。精密な天文学的計算の結果、「天の川銀河」だけでも10万光年あり、我々の銀河系よりはるかに大きな銀河が100万個も存在することがわかっています。そのひとつがアンドロメダ銀河で、天の川銀河から約250万光年の距離にある最も近い銀河です。

 

約6,500万光年の彼方、私たちの仲間である宇宙人天文学者は、おとめ座銀河団の中のどこかの銀河にいるはずです。彼らが地球を見返すためには、相当な大きさの望遠鏡が必要です。その望遠鏡がどのくらいの大きさであるべきかについては、また別の機会にお話します。

 

その前に、すべての望遠鏡の基本原理を理解しましょう。光子は電磁場の素粒子であり、単に光と呼ぶこともあります。太陽が無数の小さなボールを抱えていて、そのボールを四方八方に放出し続けていると想像してみましょう。これが、お話ししている光子のことです。

 

私たちが身の回りのほとんどのものを見ることができるのは、この光子のおかげです。しかし、遠くに行けば行くほど、目で捉えることのできる光子の数は少なくなっていきます。宇宙望遠鏡は、この光子の集まりである「宇宙のボール」を捕まえて、より小さな集光器に投影することで遠方の観測を行うため、基本的には大きな望遠鏡ほど遠くまで見ることができるのです。

 

話を戻すと、宇宙人が地球だけでなく、恐竜を観測するためには、どの程度の大きさの望遠鏡が必要なのでしょうか。そこで、彼らが必要とするレンズの直径を求めてみましょう。そのためには、角度分解能【2つの近接した天体を識別できる最小の角度】の公式を使えばいいのです。

 

角度分解能＝1.22×波長／レンズの直径

 

この式に値を入れて解くと、レンズの直径は（5.8×1010）となり、太陽から水星までの距離のほぼ半分となります。そして、それは地球を1つの点としてしか見ることができません。

 

恐竜を点として見るとしても、直径4.4光年（ケンタウルス座α星と太陽の間の距離）という巨大なレンズを作らなければなりません。

 

これは同じ式を使って、違う数字を入れてみた結果です。地球の直径の代わりに、恐竜の長さを使うのです。中生代白亜紀後期に北米に生息した、トリケラトプスは全長約9メートル、ティラノサウルスは約14メートルなので、中央値として10メートルを使って簡単に計算できるようにしました。地球に話を戻すと、現代の科学技術をもってしても、遠い銀河の惑星はおろか、我々の銀河系の惑星もほとんど検出できません。

 

ともあれ、これほど巨大な望遠鏡の建設が可能かどうかについては、もう議論するまでもないでしょう。アインシュタインは相対性理論で、物質がどのように時空を曲げていくかを説明しています。

 

質量が増えれば増えるほど、時空は曲がっていき、やがてブラックホールとなります。直径4.4光年のガラスの望遠鏡などあり得ません。半径14光分【1光分は約1800万キロメートル】の円形のガラスでさえ、ブラックホールになるには十分な質量を持つことになります。

 

つまり、地球から一定の距離にいる宇宙人は、理論的には6,500万年前に存在した恐竜を見ることができるものの、悲しいかな、あるいは幸運にも、そのための手段を手に入れることはできないのです。