黄金比や三分割法等UXデザイナーが知っておくべき数学の３大法則を簡単解説！

UXデザイナーのあなたは、おそらく数学が嫌いでしょう。芸術やデザイン方面を学んできたデザイナーたちにとって、数学は正反対の学問だからです。

しかしデザイナーがペンやブラシを走らせるとき、知らず知らずのうちに数学を活用しているのです。

今回はUXデザイナーが知るべき数学の3つの法則についてご紹介します。

 

 

1.黄金比

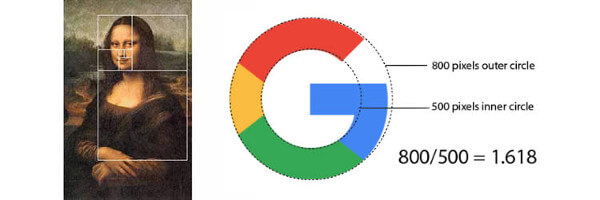
あのモナリザからGoogleのロゴまで、黄金比は幅広く使われています。下の図で、aとbの比がbとa+bの比に等しくなることを言います。

 

 

幸運なことに、デザイナーたちはもっとシンプルな理解で黄金比を活用することができます。下の四角のように、黄金比で分割されたものは人間の目に非常に美しく見えるようになります。

 

 

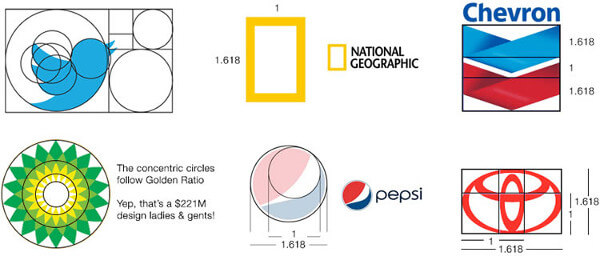
Googleのロゴにおいては2つの円の円周の比が黄金比になっています。Google以外にもロゴに黄金比を利用している企業はたくさんあります。

 

 

 

 

2.フィボナッチ数列

フィボナッチ数列は、次の数が前2つの数の和となっている数列です。0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144……と続きます。これはフィボナッチデザインの基礎となっており、ブログなどコンテンツ重視のサイトにおいて役立ちます。ひとつ例を見てみましょう。

 

シンプルながらもよくデザインされたブログです。コンテンツの配置やフォントサイズ、分割の割合まで美しく見えます。フィボナッチデザインを利用するとこうしたサイトを作ることができます。

 

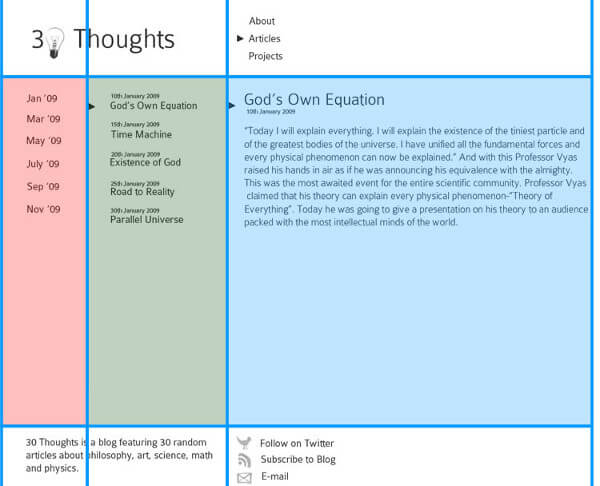
それぞれの列幅がフィボナッチ数列の比になっているのがポイントです。

 

 

 

3.三分割法

これはデザイン以外の分野でも知名度が高いため、きっとどこかで聞いたことがあるでしょう。縦を同じ長さで3分割、横も同じ幅で3分割することで作ります。

 

するとこのように縦と横の線が交差する点が4つできます。この4点は目立たせたい要素を配置する場所としてぴったりです。ウェブデザインでは左上の交点が最も重要で、人間の目がウェブページのうち最初に目にするのがそこだと言われています。

 

 

 

全てのデザインがこうした法則を守るべきかといえば、そんなことは全くありません。これらの法則はテンプレートというよりはあくまでガイドラインであり、厳守すべきものとは違います。しかし優れたUXデザイナーがこうした法則を上手に活用しているのも事実です。迷ったときの手がかりやあなたのデザインの基礎として取り入れてみてください。

 

 

 

※本記事は、3 Things Math Class Taught You About UXを翻訳・再構成したものです。